Regression analysis is a powerful tool for assessing fair lending risk and performance. As is the case with any tool, however, it must be understood and used correctly. This includes understanding the limitations which in turn defines what conclusions can be drawn from an analysis.
A fair lending regression model is merely an equation. As with any equation, it relies on a set of assumptions. The validity and accuracy of the estimates produced (known as parameters) depends on the extent to which these assumptions are satisfied. Since it is mathematical, the model offers precision but is restricted to a finite space. The equation can only produce calculations based on the inputs provided.
As researchers across disciplines understand, economic and human behavior does not always fit neatly into an equation. Quantification of measured variables is also often a challenge, and universally limited data is a constant hindrance. In the real world, satisfying all the assumptions perfectly is rarely possible.
One common issue in fair lending regression analysis is the bias that can be introduced by important variables being omitted from the model. This can occur for a number of reasons but is common in underwriting and steering analyses.
Specifically, in regard to fair lending, this type of bias can indicate discrimination exists when it actually does not. This can occur when a relevant variable is left out of the model, and it is correlated with the protected class status being evaluated.
To illustrate this, below are the results of a simulation where we create a dataset in which discrimination does not exist. The scenario is loan pricing, with zero difference between how loans were priced for the target and control group with respect to the hypothetical lender’s pricing matrix. (Through simulation we know what the outcome should be since the data is artificially generated.)
In this example, the relevant variables are DTI, LTV, and credit score. The table below shows the data and model where there is no discrimination present; that is, pricing differences are fully explained by DTI, LTV, and credit score.
The table shows the disparity between the target and control group and the percentage of times the models find discrimination in a correctly specified model versus a model that leaves out LTV and DTI. The percentage is based on the number of simulations. We conducted four different tests, running 1,000 simulations of sample sizes of 100, 500, 1,000, and 5,000.
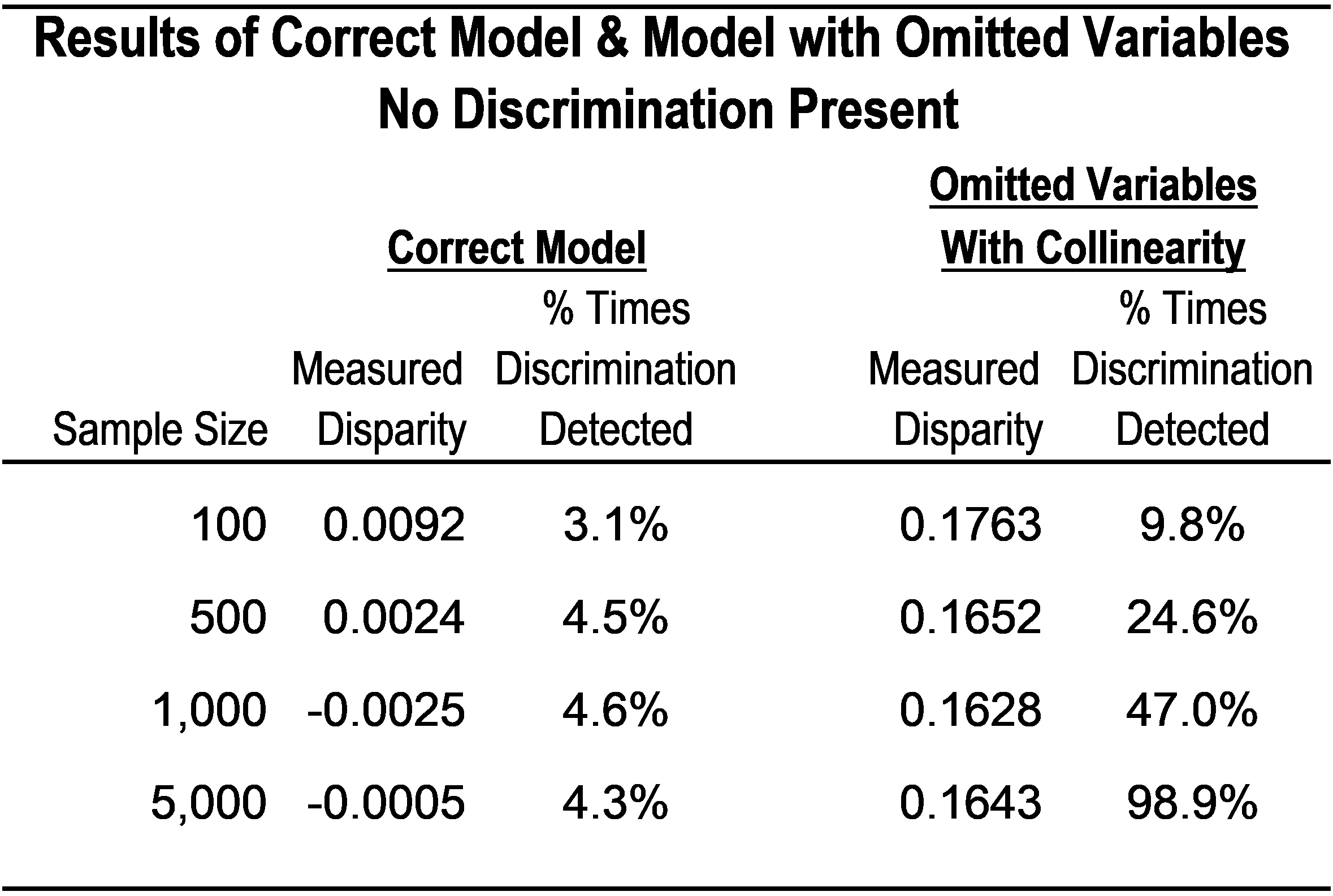
As shown above, with the model specified correctly, the measured disparity is basically zero, and discrimination is detected in < 5% of the samples. In the model with variables omitted, even though there is no disparity in the dataset, the model estimates a pricing difference of between 16 – 18 basis points between the target and control groups. The model is also most likely to find discrimination (although it does not exist) across all sample sizes; and in a sample of 5,000 observations, it detected discrimination almost 100% of the time.
In summary, there are a number of issues that can arise in fair lending regression analyses that can generate erroneous results. The case of omitted variables is just one example. In practice, data constraints are simply a reality for all disciplines with fair lending evaluations being no exception.
This does not suggest that regression analysis should not be used, but adjustments should be made to models as appropriate and analyses supplemented by other data as situations may dictate.
It is also important to qualify findings consistent with the methods employed and any subsequent limitation thereof. The goal should always be to find the right answer to the question of whether evidence of discrimination exists or not, which may not always be adequately answered by a regression model alone.



